曹亮吉/古代四大文明中,中国、埃及、巴比伦的数学发展较为人所熟悉,现在我们来看看印度;然而要读印度的数学,我们必须也要了解印度的历史。
1920年代,在印度河流域发现了古代的遗迹,使印度的历史可追溯到四千五百年前。其后的挖掘使地区扩张到现今印度的西北部与西部。在诸多的遗迹中,位于现在巴基斯坦境内的 Mohenjodaro 及 Harappa 两城市最为有名。这些城市有整齐的街道,完整的排水系统;住宅也有贵族的及各种职业人士的区分。此外还有大澡堂、谷仓等公共建筑,也有铜、青铜、铅或锡制的器皿。原住民有象形文字,可惜至今还无法解读,所以无法直接了解这支称为 Harappa 文化的历史,以及我们所关心的数学发展。然而要支撑这样高度的文明,不用说,最基本的数学是已经发展了的。
约在三千七百年前,Harappa 文化已开始式微。等到约三千五百年前,亚利安人从中亚进入印度的恒河流域时,这支文化已经消失殆尽。
亚利安人发展了世袭的种姓制度,婆罗门(教士)与武士享有统治权。婆罗门掌管知识,并且不让平民有一丝一毫的教育;为此,他们反对写作,而婆罗门教圣诗吠陀 (Veda) 则以口述承传。亚利安人在印度头一千年的历史就因文献不足而不清不楚。在数学方面,我们只能从吠陀的经文中看出,他们和别的民族一样,也在天文方面花上一些心思。
西元前六世纪,佛教兴起,屏弃了婆罗门教的闭锁性格,于是文学萌芽,历史也开始有了可靠的文献。大概也就在这个时候,出现了一类称为 Sulvasutra(用绳法则)的作品。在这些作品中,叙述了如何利用绳索,使祭坛的造型能符合宗教上的一些几何的要求,同时我们也可看出,他们已经熟知了勾股定理。
西元前326年,亚历山大大帝曾经征服了印度的西北部,使得希腊的天文学与三角学传到了印度。紧接着亚历山大大帝之后,Maurya 王朝(西元前320~185年)兴起,在其阿育王时代(西元前272~232年)势力达到顶峰,领土不但包括印度次大陆的大部分,而且远如阿富汗都在其控制之下。阿育王以佛教为国教,每到一重要城市总要立下石柱。从数学的眼光来看,这些石柱让人感到与趣,因为在石柱上我们可以找到印度阿拉伯数字的原形。
Maurya 王朝之后,印度又分崩成许多小王国,直到西元第四世纪,印度北部才又统一在 Gupta 王朝(320~550年)之下。在 Gupta 时期,许多富有城市兴起,许多大学成立,使得印度成为文化的中心。印度史上第一件天文方面的重要著作:《Surya Siddhanta》(来自太阳的知识),就产生在第五世纪初。从此以后的许多天文作品都含有三角学及三角函数。也就是从这时期开始,数学不再依附宗教礼节,而变成天文学的重要工具。
从 Gupta 王朝的晚期开始,印度又一再受到外族入侵、内部纷争的影响。从来就没有独立统一的局面。然而从六世纪开始到十二世纪为止,却产生了几位值得注意的数学家,如 Aryabhata(六世纪)、Varahamihira(六世纪)、Brahmagupta(七世纪)、Mahavira(九世纪)、Bhaskara(十二世纪)等。
从八世纪开始印度教兴起,同时回教势力也开始侵入,佛教在两者夹攻之下逐渐式微。到了西元1200年左右,佛教在其出生地的印度差不多就完全消失了。这种宗教信仰的变迁,对印度的文化是有非常具大的影响的。印度的数学从此之后就停止不前。
十六世纪初,中亚的蒙古人后裔,南下印度,建立了回化的蒙兀儿帝国。到了十九世纪,英国的势力完全取代了蒙兀儿,成为印度的主宰者。这一段时期,印度虽然有比较统一的局面,但数学方面仍然没有进展。因此十二世纪的 Bhaskara 可以说是印度传统数学的最后一人。直到二十世纪初,印度数学会成立(1907年),出版学会杂志(1909年),而且又产生了数学怪才Ramanujan(1887~1920年, 1 ),印度的数学终于渐有起色,而投入了世界数学的发展洪流中。
在印度的传统数学中,三角学与几何学是深受希腊的影响的。天文学家Varahamihira说:“希腊人虽然思想不正(异教徒),但我们该尊敬他们,因为他们有着科学的训练而凌驾他人。一个婆罗门在思想纯正之外,如果还知晓科学,岂不更好?”虽然如此,印度人却只学会把三角及几何应用到天文学或简单的面积计算。于理论则毫无兴趣,所以三角与几何学在他们手中,几乎未曾有过有意义的进展。更有进者,有时他们犯了错误而不自知,譬如许多数学家认为四边形的面积公式,而忘了这只适用于圆的内接四边形。
然而印度的传统数学在算术及代数方面则有相当的成就;这些包括建立完整的十进位记数系统,引进负数的观念及计算,使代数半符号化,提供开方的方法,解二次方程式及一次不定方程式等。
印度人要陈述数学题目时,常把它弄得幻想有趣,或者编成诗句,或者加上历史背景,使得题目能够吸引人。下面是个例子:
在某个绝壁顶上,住着两位苦行者。其中一位因拥有妖术,可以在空中行走。他从山顶垂直升空一段距离,然后对准某一小镇‘走’去。另一位苦行者,则从山顶上下来,再向小镇走去。结果两者的距离相同。假设……,问……?
另一个例子:
△
林子里头树木繁茂
累累花果树枝拂地
柠檬香蕉棕榈芒果
鹦鹉布谷叫声不绝
池塘莲花蜜蜂环绕
疲累旅者欣然入林
▽
今有 63 堆数目相同的香蕉,另加7根香蕉,平均分给 23 位旅者,刚好分完。请问一堆香蕉要有多少根?
如果每堆香蕉有 x 根,每人分得 y 根,那么要解的就是 63x+7=23y 这样的二元一次不定方程式。他们的解法是这样的:将 63 与 23 做辗转相除
……
然后根据相除的结果把 63/23 写成连分数
……
将最后的 1/5 去掉,则右边的分数为 11/4,它是 63/23 的最后第二个渐近分数。由于 63 × 4 – 23 × 11 = -1,两边各乘以 7,移项后就得63 × 28+7 = 23 × 77;这是一个答案。这种求二元一次不定方程式 ax+by=c 的方法,是由 Aryabhata 引入,再由后继的数学家改进的。这种方程式若有解的话,解法的要点在于求 a/b(可假设 a,b 互质)的连分数展开,得最后第二个渐近分数 q/p,则 ,再乘以适当的倍数就好了。
除了一次不定方程式外,现在世界通用的印度阿拉伯数字在其发源地的历史,也值得做深入一点探讨。
前面说过,在西元前五百年之前,有关印度的文献是不足的。因此我们只能从后来的文献推测早期印度人的数字观念。
印度人对抽象的数目有所偏好,他们认为要尊崇神只圣人,最好赋予一些数目。关于佛祖,有如下的说法:“佛祖有32种主要象征及80种次要象征来代表他;他的母亲32种,他要出生的房子8种。他的母亲 Maya-Devi 王后有一百万名侍女。成千上万的圣者智者会来朝佛。他的王座是花了成亿个 Kalpas 世代(一世代为43亿2千万年)的精工细琢的成品。在孕成佛祖那晚绽开了的莲花,其花瓣伸展到6千8百万哩之外。”
在记述佛祖行谊的《Lalitavistara》中,提及佛祖青年时,为了求婚而展现的数数才能。他不但能数到10的421次方,而且也能数出三百万个世界中的原子总数2 。在印度的古典文学名著《Mahabharata》(Bharata 宫廷故事)中,也时常提及古代英雄在数数目方面的本事。
不论这些故事的真实性,我们可确定它们的作者对数目都有丰富的想像力,而且对十进位以及数数目可以无穷延伸的原理,都有了相当的了解。然而在古代的梵语中,20、30、……、90,在进位体系未成熟前就已出现,其说法及符号与个位数的没有绝对的关联,这是从有位名进步到无位名的十进位位置定值法的一个障碍。一直到西元六百年左右,九个个位数字加上一个零就可以表示一切数目的想法,才趋于成熟。
印度的梵文早期用的是婆罗门文字,因此数字也是婆罗门。在九世纪阿拉伯人 Alkwarizmi 正式引介到阿拉伯之前,这些数字已经有了一些演变,它们可以用 Gvalior 庙宇上的刻文为代表。Gvalior 数字在印度本土则再次演变成 Devanagari 数字(见图二)。Devanagari 是一种字母,现在的印度文及相关的语系都是用其衍生的字母的。Gvalior 数字传到阿拉伯,其后分成东、西两支,西阿拉伯所用的数字终于演变成今日通行于世界的阿拉伯数字(见图三)。
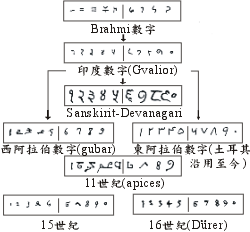
图三:印度阿拉伯数字的演变系谱
现在的印度大体上用的是阿拉伯数字,而古老的 Devanagari 数字虽然偶而用及,但其主要的流行地区是在尼泊尔等地 3 。
(部分图片见原文)
http://episte.math.ntu.edu.tw/articles/sm/sm_18_01_1/index.html



